História dos Números Complexos

Historicamente, os números complexos começaram a ser estudados graças à grande contribuição do matemático Girolamo Cardano (1501-1576). Esse matemático mostrou que mesmo tendo um termo negativo em uma raiz quadrada era possível obter uma solução para a equação do segundo grau: x² – 10x +40 = 0. Essa contribuição foi de grande importância, pois até então os matemáticos não acreditavam ser possível extrair a raiz quadrada de um número negativo. A partir dos estudos de Girolamo Cardano, outros matemáticos estudaram sobre esse impasse na matemática, obtendo uma formalização rigorosa com Friedrich Gauss (1777-1855).
O conjunto dos números complexos é o conjunto que possui maior cardinalidade, afinal ele contém todos os outros conjuntos. É necessário, pois, compreender os processos das operações (aritméticas, trigonométricas, algébricas) envolvendo elementos desse conjunto, assim como a representação geométrica dos números complexos.
Portanto, nessa seção serão abordados assuntos como: concepções básicas do número complexo, operações aritméticas com números complexos, operações trigonométricas com os números complexos, o Plano de Argand-Gauss, entre outros artigos que se relacionam com os números complexos – números de grande importância e aplicabilidade.

Progressões Geométricas (P.G)

Dizemos que uma sequência numérica constitui uma progressão geométrica quando, a partir do 2º termo, o quociente entre um elemento e seu antecessor for sempre igual. Observe a sequência:

(2, 4, 8, 16, 32, 64,...), dizemos que ela é uma progressão geométrica, pois se encaixa na definição dada.

4 : 2 = 2
8 : 4 = 2
16 : 8 = 2
32 : 16 = 2
64 : 32 = 2

O termo constante da progressão geométrica é denominado razão.

Muitas situações envolvendo sequências são consideradas PG, dessa forma, foi elaborada uma expressão capaz de determinar qualquer elemento de uma progressão geométrica. Veja:

Com base nessa expressão, temos que:

a₂ = a₁ * q
a₃ = a₁ * q²
a₅ = a₁ * q⁴
a₁₀ = a₁ * q⁹
a₅₀ = a₁*q⁴⁹
a₁₀₀ = a₁*q⁹⁹


Exemplo 1

Em uma progressão geométrica, temos que o 1º termo equivale a 4 e a razão igual a 3. Determine o 8º termo dessa PG.

a₈ = 4 * 3⁷
a₈ = 4 * 2187
a₈ = 8748

O 8º termo da PG descrita é o número 8748.

Exemplo 2

Dada a PG (3, 9, 27, 81, ...), determine o 20º termo.


a₂₀ = 3 * 3¹⁹
a₂₀ = 3 * 1.162.261.467
a₂₀ = 3.486.784.401


Soma dos termos de uma PG

A soma dos termos de uma PG é calculada através da seguinte expressão matemática:

Exemplo 3

Considerando os dados do exemplo 2, determine a soma dos 20 primeiros elementos dessa PG.

Exemplo 4

Uma dona de casa registrou os gastos mensais com supermercado durante todo o ano. Os valores foram os seguintes:

Janeiro: 98,00
Fevereiro: 99,96
Março: 101,96
Abril: 104,00
Maio: 106,08

Calcule o gasto anual dessa dona de casa, considerando que em todos os meses o índice inflacionário foi constante.

Os termos estão em progressão geométrica, observe:

106,08 : 104 = 1,02
104 : 101,96 = 1,02
101,96 : 99,96 = 1,02
99,96 : 98,00 = 1,02

A razão dessa progressão geométrica é dada por 1,02, isto indica que a inflação entre os meses é de 2%. Vamos determinar a soma dos gastos dessa dona de casa, observe:

Os gastos da dona de casa com compras de supermercado, foram equivalentes a
R$ 1.317,39.

Progressões Aritméticas (P.A)

            A sequência numérica onde, a partir do 2º termo, a diferença entre um número e seu antecessor resulta em um valor constante é denominada de Progressão Aritmética. O valor constante dessa sequência é chamado de razão da PA. Observe:

2, 5, 8, 11, 14, 17, 20, 23, 26, 29, 32, 35, 38, 41, 44, ...
5 – 2 = 3
8 – 5 = 3
11 – 8 = 3
14 – 11 = 3
17 – 14 = 3
20 – 17 = 3
23 – 20 = 3
26 – 23 = 3
29 – 26 = 3
Observe que nessa sequência a razão possui valor igual a 3.
Em uma progressão aritmética podemos determinar qualquer termo ou o número de termos com base no valor da razão e do 1º termo. Para tais cálculos, basta utilizar a seguinte expressão matemática:

an = a1 + (n – 1) * r

Exemplo 1
Sabendo que o 1º termo de uma PA é igual a 2 e que a razão equivale a 5, determine o valor do 18º termo dessa sequência numérica.
a18 = 2 + (18 – 1) * 5
a18 = 2 + 17 * 5
a18 = 2 + 85
a18 = 87
O 18º termo da PA em questão é igual a 87.
Em algumas situações ocorre a necessidade de determinar o somatório dos termos de uma progressão aritmética. Nesses casos a expressão matemática  determina a soma dos termos de uma PA.
Exemplo 2
Na sequência numérica (–1, 3, 7, 11, 15, ...), determine a soma dos 20 primeiros termos.
Cálculo da razão da PA
3 – (–1) = 3 + 1 = 4
7 – 3 = 4
11 – 7 = 4
15 – 11 = 4
Determinando o 20º termo da PA
a20 = –1 + (20 – 1) * 4
a20 = – 1 + 19 * 4
a20 = – 1 + 76
a20 = 75
Soma dos termos

A soma dos 20 primeiros termos da PA (–1, 3, 7, 11, 15, ...) equivale a 740.

Função Modular

Função é uma lei ou regra que associa cada elemento de um conjunto A a um único elemento de um conjunto B. O conjunto A é chamado de domínio da função e o conjunto B de contradomínio. A função modular é uma função que apresenta o módulo na sua lei de formação.

De maneira mais formal, podemos definir função modular como:
f(x) = |x| ou y = |x|

A função f(x) = |x| apresenta as seguintes características:

f(x) = x, se x≥ 0

ou

f(x) = – x, se x < 0

Essas características decorrem da definição de módulo.

Exemplo 1. Construa o gráfico da função f(x) = | –x|
Solução: primeiro vamos analisar o gráfico da função acima sem a utilização do módulo na sua lei de formação, ou seja, vamos fazer o gráfico de g(x) = – x


O módulo presente na lei da função faz com que a parte do gráfico que se localiza abaixo do eixo x “reflita” no momento em que toca o eixo x. Mas por quê? Simples, a parte do gráfico abaixo do eixo x representa os valores negativos de y e, como o módulo de um número é sempre um valor positivo, o gráfico de f(x) = |– x| fica:

A parte do gráfico que está azul é parte que sofreu ação do módulo.

Exemplo 2. Construa o gráfico da função f(x) = |x² – 3x|
Solução: pela definição de módulo, temos que:
f(x) = x² – 3x, se x≥ 0
e
f(x) = – (x² – 3x), se x<0
Daí, segue que:
x² – 3x = 0
x = 0 ou x = 3, logo :

Temos também que:
– (x² – 3x) = 0
x = 0 ou x = 3

Daí, segue que:

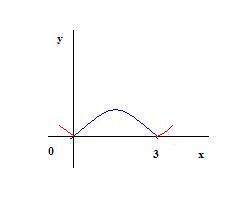
Unindo as partes dos dois gráficos que se encontram acima do eixo x teremos o gráfico da função f(x) = |x² – 3x|